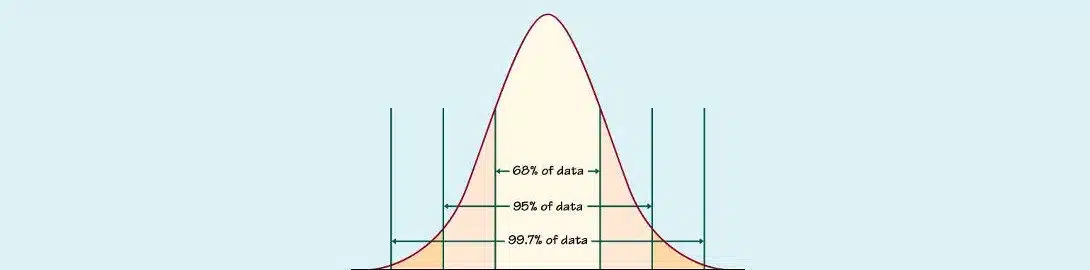
Odchylenie standardowe (standard deviation) to klasyczna miara zmienności i obok średniej arytmetycznej najczęściej stosowane pojęcie statystyczne. Zostało ono wprowadzone przez pioniera statystyki, Karla Pearsona w 1894 r.
Odchylenie standardowe zmiennej losowej oznacza się przez σ (małe greckie sigma) i definiuje jako pierwiastek kwadratowy wariancji.
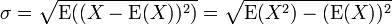
σ – odchylenie standardowe, E(X) – wartość oczekiwana zmiennej X, X – zmienna losowa
Odchylenie standardowe mówi, jak szeroko wartości jakiejś wielkości (takiej jak np. wiek, inflacja, kurs akcji, …) są rozrzucone wokół jej średniej. Im mniejsza wartość odchylenia tym obserwacje są bardziej skupione wokół średniej, im większa wartość tym większe zróżnicowanie populacji.
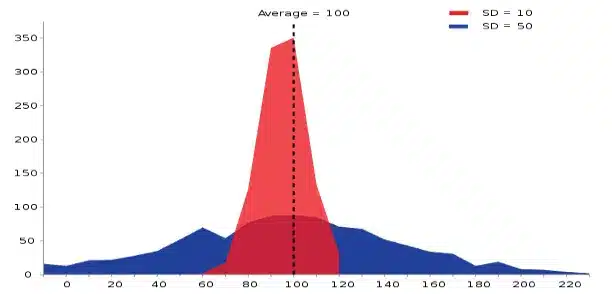
Przykład dwóch populacji o tej samej średniej (100), ale różnych standardowych odchyleniach (10 i 50).
Przykład
Aby lepiej zrozumieć czym jest odchylenie standardowe i dlaczego jest ważne rozważmy poniższy przykład.
Wyobraź sobie, że zbadaliśmy dwie grupy osób pod względem ich wieku. Wiek osób w grupie A rozkłada się następująco 11, 15, 18, 20, 21, 24, 60, 71, 78, 82, natomiast w grupie B natomiast 36, 36, 37, 38, 39, 40, 41, 42, 44, 47. Średnia wieku dla obu grup wynosi 40 lat. Ale czy oznacza to, że są one identyczne? Czy wystarczy skorzystać ze średniej, aby móc opisać i porównać obie grupy? Odpowiedź brzmi NIE.
Korzystając ze średniej można dojść do błędnego przekonania, że grupy nie różnią się między sobą. W rzeczywistości jednak różnice są znaczące. W pierwszej grupie mamy duże różnice wiekowe. Druga grupa jest bardziej jednorodna, a wiek poszczególnych osób nie różni się znacząco.
Różnice w obu grupach pomaga nam zrozumieć odchylenie standardowe. W przypadku grupy A wynosi ono 27,5 a w przypadku grupy B 3,4 – a więc jest znacząco różne.
Odchylenie standardowe dostarcza nam informacji czy wyniki w grupie są podobne do siebie czy zróżnicowane. Im mniejsze odchylenie standardowe tym mniejsze zróżnicowanie wyników i większe skupienie ich wokół średniej. Im większe odchylenie tym większe rozproszenie wyników (a więc większe zróżnicowanie badanej grupy).